Mi SciELO
Brazilian Political Science Review (Online)
versión On-line ISSN 1981-3821
Braz. political sci. rev. (Online) vol.4 no.se Rio de Janeiro 2009
How safe are "safe" seats? A comparison of voluntary and compulsory voting systems*
Tim R. L. Fry I; Keith JakeeII; Martin KenneallyIII
IRMIT University, Australia
IIFlorida Atlantic University, USA
IIIUniversity College Cork, Ireland
ABSTRACT
Many observers have expressed concern that low voter turnout reflects an acute shortcoming in democratic politics. One proposed remedy, making voting compulsory, has garnered increasing attention among academics over recent years. Our article focuses on some of the technical properties of compulsory voting rules (CVR) while ignoring the philosophical debate over whether voting should be an obligation or a right. Using basic probability analysis, we compare a voluntary voting rule (VVR) to a compulsory one. We show that, under certain conditions, an electoral seat or district can become safer - or less competitive - with the imposition of a CVR. We also discuss some political implications of our analysis. For example, when generalized to, say, the national political system, this result implies fewer competitive seats in a CVR compared to a VVR, everything else equal. We contend that, because fewer seats will be "in play" in a CVR, CVRs should exhibit lower turnover of seats. Also, political suppliers can be expected to more narrowly focus their attention - and resources - on this smaller set of competitive seats than we would expect under a VVR.
Keywords: Compulsory voting and swing seats; Competitiveness of electoral seats; Standard deviation of expected electoral results; Narrowing of political suppliers' focus.
Introduction
While voting is not compulsory in most countries, it is more common than many think: almost 30% of democracies (18 in total) make voting compulsory (Massicotte et al. 2003). Despite its widespread implementation (especially when we include countries that have relied on compulsory voting at some point in the past), most scholarship on the topic has focused on its normative aspects.
The argument for compelling citizens to vote tends to centre on the low — and often falling — rates of voter turnout around the world. It is argued that highly variable voter participation in voluntary systems weakens the "legitimacy" of democratic institutions and therefore weakens democracy itself. Lijphart (1997, 2), among others, contends that one way to make voting more equal, and hence more "democratic", is to aim for a maximization of turnout. A close line of argument suggests that voting is really a civic duty which should be served by each citizen in return for enjoying the benefits of democracy (Lijphart 1997; Wertheimer 1975).
Those arguing against compulsion take issue with the view that voting is a duty and challenge the use of coercion by the state to enforce what they consider to be a democratic right (Abraham 1955; Jones 1954). They question the right of the state to compel a citizen to vote for a candidate with whom that citizen does not agree, or in whom he does not believe. They are also suspicious of the quality of a "democratic" outcome if it is based, at least in part, upon the opinions of an ill-informed, or apathetic section of electors who are compelled by law to vote (Hughes 1966, 83).
The more analytical exceptions to these normative approaches are largely empirical studies that examine the following: how compulsory voting rules (CVRs) affect voter turnout (see, inter alia, Jackman 1987; Massicotte et al. 2003; McAllister 1986): whether compulsory voting favours certain parties in Australia (Jackman 1999; Mackerras and McAllister 1999); and whether the relatively high level of invalid votes in Australia is attributable to compulsory voting (McAllister and Makkai 1993). There also exists a scholarly exchange over compulsory voting's effect on the growth of government (Crain and Leonard 1993; Yeret 1995; O'Toole and Strobl 1995; Crain 1995). Crain and Leonard find that CVRs slow government growth and posit that this negative relationship supports an interest group theory of government as opposed to a median voter theory of government. Jakee and Sun (2006) consider the likely effects of the role of information (including costs) on the decision to vote and, taking an expressive view of voting, investigate two unexamined claims by CVR advocates: (i) that individuals are transformed by forcing them to vote, and (ii) that a compulsory electoral outcome is a more accurate reflection of community preferences. Using a formal model, they conclude that compelling those who are not particularly interested in, or informed about, the political process to vote increases the proportion of random votes and they show that under simple majority rule, compulsory voting may violate the Pareto principle; in other words, the less popular candidate is more likely to be elected (as a random result) under a CVR.
This article aims to expand upon our technical understanding of compulsory voting rules and ignores the philosophical debate over whether voting should be an obligation or a right. In the analysis that follows, we focus on the statistical properties associated with a shift from a voluntary voting rule (VVR) to a CVR. We show that, under certain assumptions, an electoral seat or district can become safer — or less competitive — with the imposition of a CVR. When generalized to an entire political system, say the national one, this result implies fewer competitive seats in a CVR compared to a VVR. We then argue that because fewer seats will be "in play" in a CVR, political parties (and incumbent governments) will more narrowly focus their attention - and resources - on this smaller set of competitive seats than we would expect under a VVR. Our next section presents our probability analysis, while the one following discusses some political implications of our analysis. The penultimate section raises an important caveat to our results.
The Dispersion of Expected Results under a CVR and a VVR
We begin our analysis by noting that real-world CVRs tend to register higher turnout than voluntary systems, although they do not typically register a full 100% turnout. Turnout in Australia is, for example, approximately 95% (Australian Electoral Commission 2002). While our model and the analytical results are sufficiently general to encompass CVR turnout that is less than 100%, we tend to discuss our model, below, as if CVRs deliver 100% turnout. We do this for ease of exposition: it is simply more straightforward to illustrate examples using, say, 100 voters representing the entire eligible voting population (i.e., 100% turnout under a CVR) and compare this setting to some smaller turnout, say, 64, under a VVR. The VVR turnout can then be easily calculated as a percentage (i.e., 64%) of the total CVR turnout.
Throughout our analysis we assume that there are only two candidates (representing two parties), denoted 1 and 2, and that these candidates run for office in a single-member district using simple majority voting. Imagine a scenario under a VVR in which we know the percentage of the vote that is expected to go to each candidate. These expectations are typically formed through pre-election attempts to predict the election's outcome using a variety of means, such as opinion polls, previous election results, and more recently even Internet-based betting markets. For examples of the latter in the United States, see Intrade (n.d.), or the University of Iowa's Iowa Electronic Markets (n.d.).
We introduce several variables and their definitions:

For clarity of exposition, we will assume throughout our analysis that candidate 1 is the leading candidate (i.e., p1 > p2) unless the candidates are tied (i.e., p1 = p2). We can therefore characterise candidate 2 as the trailing or "underdog" candidate.
Standard deviation and variance are used in the conventional sense of measuring the variability or dispersion of a result. Specifically, we focus on standard deviation to measure the variability of the expected result p1. In other words, we are interested in comparing the variability of the expected vote share (a percentage) for the winning candidate, candidate 1, under a VVR and a CVR. Formally, these standard deviations (of proportions) are defined as:
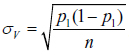 , and (1)
, and (1)
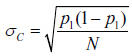 . (2)
. (2)
The difference between ÏV and ÏC lies in the assumption that all eligible citizens, N*, are legally obliged to vote under a CVR (i.e., N ≡ N*), whereas only some fraction of these, n/N, do so under a voluntary system. By definition, then, n < N. As noted above, we assume hereafter for expository clarity (but without loss of generality) that N = N*, i.e., that 100% of the electorate votes under CVR.
Taking the ratio of ÏV to ÏC allows us to directly compare the standard deviations under each rule regime:
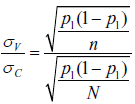 . (3)
. (3)
After rearranging terms, we arrive at an expression for the standard deviation of p1 under the CVR in terms of the VVR one:
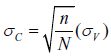 . (4)
. (4)
This is a reasonably strong result that tells us that the standard deviation of the vote share of candidate 1 will be lower under a CVR than it will under a VVR, as long as turnout is smaller in a VVR than a CVR (i.e., that is n < N). Employing values that are easily calculated, we can imagine the number of all eligible citizens, N = 100, and the number who actually turn out in a VVR, n = 64; then 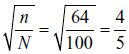 . The resulting dispersion in the CVR, ÏC, would be 4/5 the value of the dispersion of p1, ÏV, under a VVR. This result can be readily seen in Figure 1, which plots the probability distributions representing each of our two examples under VVR and a CVR.1
. The resulting dispersion in the CVR, ÏC, would be 4/5 the value of the dispersion of p1, ÏV, under a VVR. This result can be readily seen in Figure 1, which plots the probability distributions representing each of our two examples under VVR and a CVR.1
Note, moreover, that in addition to the lower dispersion for the CVR, Figure 1 illustrates that the probability of candidate 1 losing the election has fallen. This result follows from the fact that the area under either frequency distribution to the left of any value of p1 measures the probability associated with that value of p1. Thus, the area under each curve to the left of the vertical line drawn through p1 = 0.5 measures the probability that candidate 1 will lose the election, or receive less than 50% of the vote. Under a VVR, Figure 1 shows that the probability of candidate 1 actually losing the election is the area A + B. On the other hand, the area under a CVR is only B, which clearly illustrates that the probability that candidate 1 will lose the election under the CVR has fallen.
We can also characterise the relationship between the two systems in terms of the likelihood that candidate 2 might catch up with candidate 1 in order to tie the election. This can be formalised in the following manner:
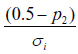 . (5)
. (5)
The numerator in equation (5) is simply the percentage candidate 2 needs to tie with candidate 1 and the denominator is the relevant measure of dispersion under each rule regime (i.e., Ïi = ÏV, or Ïi = ÏC). This ratio yields the distance candidate 2 is from tying the election result in standard deviations.
To take an example, imagine that p1 = 60% and therefore p2 = 40% under a VVR. Suppose further that ÏV = 5%. Inserting these values into equation (5) suggests that 0.10/0.05 = 2. In other words, candidate 2 is 2 standard deviations away from tying; making up 2 standard deviations of distance between himself and candidate 1 is highly unlikely since values at 2 standard deviations and beyond are commonly considered outside the "normal" range.
Now, consider the same example under a CVR; we expect ÏC < ÏV, as demonstrated in equation (4). In this case, the 10% numerator, (0.5 - p2), is divided by the CVR's smaller standard deviation (i.e., 4/5(ÏV) = 4%) and the entire ratio must therefore increase. Thus, 0.10/0.04 = 2.5, implying that candidate 2 now has to make up 2.5 standard deviations of distance to tie the race under the CVR. The "distance" needed for the losing candidate to tie the race has increased under the CVR by 25% (i.e., 0.5 standard deviations increase under CVR divided by the 2.0 standard deviations under the VVR).
Political Implications
The forgoing analysis shows that, other things constant, the certainty of the expected result of a typical seat or electorate will increase under a CVR. This is a key insight because reducing the uncertainty (viz. standard deviation) associated with the outcome of a given seat must be valued by political suppliers as it allows them to distinguish between races that "matter" versus those that do not. In other words, while the "competitiveness" of seats is typically defined in terms of the (small) difference between candidate 1's and candidate 2's expected vote, i.e., p1 - p2 ≈ 0, our results emphasise the certainty of that difference.2 For example, the increase in certainty that a CVR can potentially deliver means that even a close or competitive race under a VVR, in which p1 - p2 was small, might not be considered close under a CVR if the standard deviation fell sufficiently to increase the certainty of the outcome, regardless of the proximity of p1 to p2.
Moreover, the degree of safeness will increase under a CVR when the distance between VVR turnout and CVR turnout is larger, everything else constant. For example, compare two different electorates, each with identically small (p1 - p2); suppose the difference between p1 and p2 is 5%. Further suppose that VVR turnout in seat A is low, whereas VVR turnout in seat B is very high. From equation (4), it can be verified that the CVR makes both seats safer, but it has only a small effect on seat B compared to a larger effect in seat A. The result is that all seats become safer under a CVR, but less so for high turnout VVR marginal seats.
If we use our results to generalise to all electorates within a given regime, say at the national level, we contend that the number of competitive electorates, when defined in terms of both (p1 - p2) and certainty of the expected result, will fall under a CVR. Put differently, we expect the percentage of "safe" seats to increase as we move from a VVR to a CVR. Holding everything else constant, elections should therefore be decided by fewer competitive seats in a CVR.
One empirically testable implication of this result is that we would expect CVRs to be more "stable" than VVRs. By stability, we mean, specifically that, other things constant, (i) CVRs are expected to have a smaller turnover of seats, and (ii) the seats that do "swing" are those that would have had a small (p1 - p2) under high VVR turnout (recall that "close" races under a VVR with high turnout are expected to remain the "closest" when converted to a CVR).
The increase in the percentage of safe electorates across the political system raises a final implication of our analysis. As many observers have noted, an important electoral strategy for political parties and incumbent governments is to focus resources on the most competitive seats. See, for example, Fleck (1999), Levitt and Snyder (1997), or Wright (1974) for empirical analyses using U.S. data, or Denemark (1998) using Australian data. This hypothesis is also consistent with what Dixit and Londregan (1996) call the "swing voter" outcome.
Our results suggest that while both systems generate incentives for political suppliers to concentrate on the most competitive seats, the focus of that concentration will be narrower in a CVR because of the fewer number of truly competitive seats. This suggests a greater concentration of political resources, both financial and non-financial, on the relatively smaller number of "close" races. This assertion applies, of course, to the activity of incumbent governments, since they have control of the public purse, or what has been called "pork". Indeed, one of the most well recognized advantages of incumbents is their potential to direct government resources in ways that may affect voting outcomes.
Limitations of our Analysis: IIA
Our analysis makes a key assumption concerning those voters who abstain under a VVR, but are compelled to vote under a CVR, namely that they will vote for candidates 1 and 2 in the same percentages as the voters do who turnout under a VVR. In other words, our results depend on the common statistical assumption, independence from irrelevant alternatives (iia). Given that we do not have any a priori grounds for assuming the voting intentions of abstainers differ from those who vote, we do not regard this as an unreasonable working hypothesis. On the other hand, if the latent political preferences of abstainers differ substantially from those preferences exhibited by voluntary voters, then our analytical framework, which focuses on how turnout relates ÏC to ÏV, would have to be broadened to incorporate how turnout might effect (p1 - p2) under a CVR.
Conclusion
We employed some basic probability analysis in order to compare the degree of certainty in the ex ante probabilities associated with two candidates in voluntary and compulsory voting regimes. Using the definition of the standard deviation of the proportion who are expected to vote for candidate 1, p1, we showed that, other things constant, the expected result for a typical seat or electorate becomes more certain under a CVR. This finding is noteworthy because reducing the uncertainty of electoral outcome must be valuable to political suppliers: it allows them to better determine which races "matter". This certainty of electoral outcome allows us to broaden the definition of a "competitive" seat, which is typically thought of only in terms of a small difference between candidate 1's and candidate 2's expected vote, i.e., p1 - p2 ≈ 0. Our results emphasise that the certainty of that difference might be equally valuable to knowing the respective probabilities for each candidate. As we noted, this certainty value implies that even a close or competitive race under a VVR (i.e., one in which p1 - p2 was small) might not be considered as close under a CVR if the standard deviation fell sufficiently to increase the certainty of the outcome, regardless of the proximity of p1 to p2.
We also argued that if we generalise our results to all electorates within, say, a national electoral system, that the number of competitive electorates, when defined in terms of both (p1 - p2) and certainty of the expected result, will fall under a CVR (and thus the percentage of safe seats will increase). As a result, we can infer that elections might be decided by fewer competitive seats in a CVR. If political suppliers focus resources on the more competitive seats, as many observers have suggested, we can expect that they will more narrowly focus their attention and resources on a smaller subset of the citizenry in a CVR than they would have to in a VVR.
An empirically testable implication of our analysis is that CVRs are expected to be more "stable" than VVRs. We define "stability" in the sense that CVRs should have a smaller turnover of seats, and that the seats that do change are expected to be the ones that would have been "close" (i.e., a small (p1 - p2)) under high VVR turnout.
Finally, we noted that our analysis depends on a common assumption in statistical inference, the independence of irrelevant alternatives. That is, we assume that the abstainers in a VVR who are forced to vote in a CVR would vote in the same percentages as do the electors who vote voluntarily under the VVR. The opinion polls from which (p1 - p2) is often established typically survey random electoral samples of those who vote and those who abstain so this assumption seems reasonable as an initial hypothesis. However, this assumption does warrant further theoretical and empirical analysis.
Notes
1 Our Figure 1 employs the normal distribution even though our example is that of a binomial distribution. The normal distribution is visually easier to comprehend and sufficiently approximates the binomial when n is large.
2 Besides being described as "close", competitive seats are also commonly referred to as "swing" or "marginal" seats. Note also that the standard definition of competitiveness (p1 - p2) is related to the numerator in equation (5) by a factor of 2; specifically, (p1 - p2) = 2(0.5 - p2).
Bibliographical References
Abraham, Henry. 1955. Compulsory voting. Washington DC: Public Affairs Press.
Australian Electoral Commission (AEC). 2002. Voter turnout 1901-2001 (National Summary). http://www.aec.gov.au/Elections/Australian_Electoral_History/Voter_Turnout.htm (accessed November, 2009).
Crain, W. Mark. 1995. The right versus the obligation to vote: Rejoinder to Yeret, and O'Toole and Strobl. Economics and Politics 7 (3): 281-287.
Crain, W. Mark and Mary Leonard. 1993. The right versus the obligation to vote: Effects on cross-country government growth. Economics and Politics 5 (1): 43-52.
Denemark, David. 1998. Buying votes: Parliamentary systems and pork barrel politics. Australian Quarterly 70 (6): 37.
Dixit, Avinash and John Londregan. 1996. The determinants of success of special interests in redistributive politics. The Journal of Politics 58 (4): 1132-1155.
Fleck, Robert. 1999. Electoral incentives, public policy, and the new deal realignment. Southern Economic Journal 65 (3): 377-404.
Hughes, Colin. 1966. Compulsory Voting. Politics 1 (2): 81-95.
Intrade. n.d. Intrade: The prediction market. Dublin, Ireland. http://www.intrade.com/ (accessed November, 2009).
Iowa Electronic Markets. n.d. What is the IEM? Iowa City, Iowa: University of Iowa. http://www.biz.uiowa.edu/iem/index.cfm (accessed November, 2009).
Jackman, Robert. 1987. Political institutions and voter turnout in the industrial democracies. American Political Science Review 81 (2): 405-423.
Jackman, Simon. 1999. Non-compulsory voting in Australia? What surveys can (and can't) tell us. Electoral Studies 18: 29-48.
Jakee, Keith, and Guang-Zhen Sun. 2006. Is compulsory voting more democratic? Public Choice 129 (1): 61-75.
Jones, W. H. Morris. 1954. In defence of apathy: Some doubts on the duty to vote. Political Studies 2(1): 25-37.
Levitt, Steven, and James Snyder. 1997. The impact of federal spending on house election outcomes. Journal of Political Economy 105 (1): 30-53.
Lijphart, Arend. 1997. Unequal participation: Democracy's unresolved dilemma. American Political Science Review 91 (1): 1-14.
Mackerras, Malcolm and Ian McAllister. 1999. Compulsory voting, party stability and electoral advantage in Australia. Electoral Studies 18 (2):217-233.
Massicotte, Louis, Andre Blais, and Antoine Yoshinaka. 2003. Establishing the rules of the game: Election laws in democracies. Toronto: University of Toronto Press.
McAllister, Ian. 1986. Compulsory voting, turnout and party advantage in Australia. Politics, 21 (1): 89-93.
McAllister, Ian, and Toni Makkai. 1993. Institutions, society or protest? Explaining invalid votes in australian elections. Electoral Studies 12 (1): 23-40.
O'Toole, Francis, and Eric Strobl. 1995. Compulsory voting and government spending. Economics and Politics 7 (3): 271-280.
Wertheimer, Alan. 1975. "In defense of Compulsory Voting." In Participation in Politics, ed. J. Roland Pennock and John Chapman. New York: Lieber-Atherton.
Wright, Gavin. 1974. The political economy of new deal spending: An econometric analysis. Review of Economics and Statistics 56 (1): 30-38.
Submitted in November, 2008
Accepted in June, 2009