My SciELO
Kriterion: Revista de Filosofia
Print version ISSN 0100-512X
Kriterion vol.2 no.se Belo Horizonte 2006
The symmetries of the Hempelian model of explanation
As simetrias do modelo hempeliano de explicação
Túlio Roberto Xavier de Aguiar1
Translated by Paulo Pimenta Marques
Translation from Kriterion, Belo Horizonte, v.46, n.111, p.138-152, Jan./June 2005.
ABSTRACT
This article critically examines Hempel's deductive-nomological model. We focus on the model's symmetries produced by requirements of nomic sufficient conditions for explanations. Such conditions, we argue, cannot translate correctly explanatory and causal relations.
Keywords: Hempel, Explanation, Causation, Sufficient Conditions
RESUMO
Este artigo faz um exame crítico do modelo nomológico dedutivo de Hempel. Nós focalizamos a atenção sobre certas simetrias desse modelo geradas pela exigência de condições nomicamente suficientes para uma explicação. Tais condições, argüimos, são incapazes de traduzir corretamente as relações explanatórias e causais.
Palavras-chave: Hempel, Explicação, Causação, Condições Suficientes
Introduction
All contemporary theories on explanation start from Hempel's work. Either to improve it or to search an alternative way, the Hempelian theory has been useful as a permanent guide to orientate any reflection on scientific explanation. In what follows, we make a critical inspection of the so called deductive-nomological model, focusing on the symmetries that characterize it.
Hempel uses the following scheme to present the deductive-nomological (N-D) model:
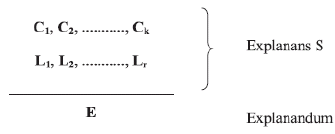
In this scheme, C1, C2, ..........., Ck describes the particular circumstances and L1, L2, ..........., Lr are the general laws that hold up the explanation. The event or fact to be explained or even the sentence that describes them are designated by E. The line indicates that we are facing a deduction from the explanans to the explanandum. That intends to express the idea that a phenomenon is explained by showing that it resulted from certain particular circumstances according to certain laws. But how exactly must this be understood in Hempel? The following passage is crucial to us to understand the spirit of the Hempelian theory:
( ) the argument shows that, given the particular circumstances and the laws in question, the occurrence of the phenomenon could be expected; and it is in this sense that the explanation enables us to understand why the phenomenon occurred. (Hempel, 1965, p. 337, italics in the original).
So Hempel explains how an explanation produces the understanding of the occurrence of a phenomenon, event or aspect of an event, showing that it was expectable. Hempel considers this a general condition of adequacy to any explanation – that the explanans makes the explanandun expectable , if this has not happened yet.2
The Symmetry Thesis
The kind of argument discussed by Hempel in connection with explanation makes him announce the thesis of the structural identity between explanation and prediction, also known as the symmetry thesis. In an initial formulation, Hempel says:
Since in a fully stated D-N explanation of a particular event the explanans logically implies the explanandum, we may say that the explanatory argument might have been used for a deductive prediction of the explanandum-event if the laws and the particular facts adduced in its explanans had been known and taken into account at a suitable earlier time. In this sense, a D-N explanation is a potential D-N prediction (Hempel, 1965, p. 366)
What is declared above constitutes half of the symmetry thesis: all adequate explanation is potentially a prediction. The other half says that "all adequate prediction potentially constitutes an explanation". Thus, explanation and prediction, according to Hempel, have identical logical structure, only diverging as to the pragmatic aspects, as what is known and what is searched, and as to the temporal relations between the events present in the explanans and in the explanandum, and between these and the time the derivation occurs. In an explanation, the explanandum-event is known and we search for the laws and particular facts that allow us to deduce it. Now, in the case of a prediction, we look at the laws and particular facts and deduce the event before it occurs. The first sub-thesis has fundamental importance for Hempel, so much so that he asserts that it is supported by a more general principle that constitutes a "a general condition of adequacy for any rationally acceptable explanation of a particular event". He enunciates this condition as follows:
Any rationally acceptable answer to the question 'Why did event X occur?' must offer information which shows that X was to be expected – if not definitely, as in the case of D-N explanation, then at least with reasonable probability (Hempel, 1965, p. 367-368).
Several objections were presented to each one of the sub-thesis. As to the first one, Scriven led strong criticisms of Hempel's model. Let's first consider the case in which we have statistical laws.3 25% of the people who get syphilis and are not treated with penicillin develop paresis. If we ask why a person has paresis, the answer seems to be the fact that he or she was a victim of non- treated-with-penicillin syphilis (apud Salmon, 1998, p. 309-310). In this case, however, the facts present in the explanans – that non-treated syphilis regularly associates itself with paresis in 25% of the cases and that a certain person was a victim of syphilis – do not allow a reasonable prediction of the explanandum – the development of paresis by a specific person. It is clear that somebody filled with deterministic faith can say that statistical laws only reflect our state of ignorance and that the subsequent investigation can reveal some other characteristics, beside the non-treated syphilis, that would restore our predictive power. We could, thus, certainly know, which individuals would develop paresis. Evidently, one pays a high price for presuming, without empirical investigation, the truth of determinism.
Hempel is sensitive to the findings of quantum theory that seems to indicate that the laws of the microphysical world are irreducibly statistical. He prefers, in this case, to say that the nomically necessary conditions for an event are not explanatory (Hempel, 1965, p. 369). Thus, he avoids presuming that the world is deterministic. An example by Salmon can help us understand the situation even better. Let us suppose the tossing of a coin that habitually results in 95% heads and 5% tails. If we toss the coin and get heads, we could build an explanation according to the Hempelian model, as long as this event can be rationally expected, given the information present in the explanans. If, however, we obtained tails, we would not be able to predict this event, given the explanans (Salmon, et al., 1992, p. 29). For Hempel, only a highly probable event can be explained. The question, here, is that, in both cases, we understand the mechanism in question equally well. It does not seem to be natural to restrict our explanatory capacity only to events that are highly probable, given the explanans.4
An example of a different nature, also by Scriven, puts the following problem: there are several explanations that, to be changed into predictions, would need the knowledge of the explanandum. One can explain the fact that a man has murdered his wife, pointing out that he is jealous of her. But, we could hardly predict the murder, even if we knew the husband's characteristic. In fact, we would have to know that the jealousy was strong enough to cause the crime, but we could only know that after the fact had occurred (Scriven, 1959, p. 579). This example allows perhaps an easier refutation by Hempel. He claims that the example does not affect the conditional that an adequate explanation could have helped to predict the explanandum if the necessary information for that had been known before the event. He also remarks that Scriven does not demonstrate, in his examples, that the kind of factor that one needs to know for prediction can not be known before the explanandum-event happens (Hempel, 1965, p. 371). The examples presented so far, specially the one of the "paresis", challenge the first sub-thesis of the symmetry. The attacks to the first sub-thesis, in general, try to show that there are genuine explanations that do not count as predictions (in the Hempelian sense) and, thus, that the adequacy to the Hampelian model is not a necessary condition for the explanatory character. Here, however, we shall only subscribe to the criticisms of the sufficiency of the deductive-nomological model.
The Insufficiency of the Nomic Sufficiency
An attack to the second sub-thesis threatens the sufficiency of the model. For, in this case, we will be facing a prediction, in Hempelian sense, which does not potentially constitute an explanation. Hempel, in fact, considers the second sub-thesis less safe than the first one. Hempel himself shows the difficulties of considering that all prediction is a potential explanation through the example of measles. One of the first symptoms of this disease is the appearance of whitened spots in the mouth's mucosa, known as "Koplik spots". Their appearance is always followed by the other measles manifestations. Thus, these ones could be predicted from those. Would such correlation, however, be explanatory? Hempel admits that there may be a doubt here, but when he tells us his reasons for such doubt, these could hardly avoid being surprising for most readers of several tendencies. He says:
Yet this case – and others similar to it – does not constitute a decisive objection against the second sub-thesis. For the reluctance to regard the appearance of Koplik spots as explanatory may well reflect doubts as to whether, as a matter of universal law, those spots are always followed by the later manifestations of measles. Perhaps a local inoculation with a small amount of measles virus would produce the spots without leading to a full-blown case of the measles. (...) the generalization that Koplik spots are always followed by later symptoms of the measles would not express a law and thus could not properly support a corresponding D-N explanation (Hempel, 1965 p. 374 – 375, my italics).
The passage shows that Hempel refuses even to make the usual distinction between cause and symptom.5 The reasons that can motivate Hempel here are quite obscure. We think of (and also Hempel in his non-philosophical moments) Koplik spots and the measles later symptoms as being common effects of the same cause – the viral infection. Speaking in causal language, two alternatives seem to be relevant in this case: a) Koplik spots can be an intermediate cause between the infection and the symptoms that appear after the spots. Now, if we do the test proposed by Hempel, that is, if we inoculate a small portion of measles virus and the Koplik spots appear without the later symptoms, then we will know that they are not nomically sufficient for later symptoms. And we should notice that , for Hempel, only nomically sufficient conditions are explanatory. The Hempian reconstruction for the cause is made through a nomic regularity, expressed by a material conditional, where the antecedent is sufficient for the consequent and the antecedent conditions are earlier in time in relation to explanandum. In short, the causation is nomic sufficiency plus temporal priority.
Going back to our example, the two descriptions in (a) and (b) can be represented respectively, by pictures 1 and 2, as follows:
Still keeping an openly causal language, we need to think of what happens if we weaken the cause, the viral infection, in the way suggested by Hempel. We can think that the causal situation is similar to the one we find in Picture 1: the Koplik spots and the other measles appearances are colateral effects of the same cause. In this case, in fact, we do not accept that there is explanatory connection between the spots and the other measles appearances, even if there is nomic sufficiency between them. On the other hand, we can imagine the situation as that presented in Picture 2, where Koplik spots work as intermediate causes; the weakening of the infectious agent might cause a weakening of the intermediate cause, avoiding the appearance of other manifestations. We would, however, be willing, in this situation, to consider Koplik spots, even if they are not sufficient, as genuine explanatory factors of the other manifestations (when they happened), even if we considered them a more superficial explanation than that which would consider viral infection as causal factor – a conclusion contrary to Hempel's. In short, in the case represented in Picture 1, we may have nomic sufficiency without having in fact an explanation. On the other hand, in the case illustrated in Picture 2, we may not have nomic sufficiency and even so have an explanation. The second case, incidentally, according to what was already discussed in the previous section, casts doubt on the need that an explanation be adequate to the Hempelian model.
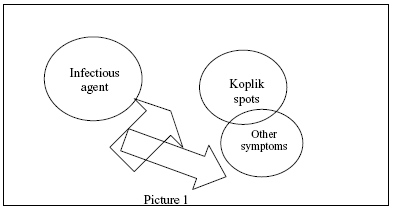
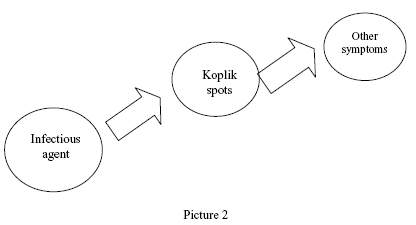
The Hempelian demand that an explanation indicates a nomically sufficient condition for the explanandum, does not allow us to discriminate between the alternatives shown in each one of the pictures, constituting a rather serious drawback. We would not know, for example, whether an intervention to prevent the Koplik spots would be effective to avoid the other measles manifestations. In order to know where to intervene, we have to know the map of causal relations, and this knowledge is fundamental to explain an event. Regularities that incorporate nomically sufficient conditions are a rough tool to assess causal and explanatory relations. In the previous citation, Hempel talks about measles later symptoms, disagreeing with the current use of the word. When we talk about symptoms, we mean, to a certain extent, collateral effects of a disease, without explanatory value. Thus, Hempel sacrifices the distinction, important in medicine, between symptoms and causes. His theory standardizes several causal distinctions, reducing them to nomic sufficiency.
In the final account, Hempel considers the second sub-thesis, that all prediction is potentially an explanation, as an open question. We must observe, however, that this is not due to the problems discussed above, concerning the example of measles. As for the predictions based on nomically sufficient conditions, we saw that Hempel, in fact, endorses the second sub-thesis. All our philosopher's hesitation is due to the possibility, mentioned by Scheffler and Scriven, that there are forms of prediction that are not based on general laws, proving themselves, therefore, to be incapable of being converted into an N-D explanation (Hempel, 1965, p. 375-376).6 Our interest, however, was to examine if there is symmetry between nomically based predictions and explanations.
The Second Thesis of the Symmetry
At this point, we shall discuss some of the classic counter-examples concerning the deductive-nomological model, evaluating its strength against the Hempelian theory. Before, however, we must take a stand as to the function of counter-examples in the evaluation of philosophical theories. We believe that philosophical theories, when possible, must be confronted with our pre-philosophical judgments. Such judgments reflect the way we determine what falls under a certain concept. We shall take the concept of science as an example. We all know typical examples of science: Newton and Galileo's physics, Lavoisier's chemistry, Darwin's theory of evolution, etc. We also know cases that we would like to leave out, like astrology, vodu, chiromancy, etc. A good theory of science must, in principle, include the first examples and exclude the last ones. If the theory does not accomplish such segregation in the indicated way, good motives must be presented as compensation. For example, a theory about a certain concept may include undesirable cases and exclude desirable ones, but it may offer advantages, such as simplicity, and the increase of the capacity of integration of the concept under exam with other concepts, reducing them to concepts which are considered more fundamental and clearer. Such theories may sacrifice the attribute of adequacy, badly reflecting pre -philosophical characteristics of the concept. It is clear that our pre-philosophical judgments may also be corrected and improved by theory. We shall have to decide, in each case, as to what direction to take to perform the adjustments and corrections. Even if in another context, talking about rules of inference, Nelson Goodman synthesizes the spirit of the commentaries made above (Principle Reflexive Balance):
(...) deductive inferences are justified for their conformity to the valid general rules, and (...) general rules are justified for their conformity to valid inferences. This is, however, a virtuous circle. The point is that the rules and the particular inferences are justified because they are placed in mutual agreement. The rule is corrected if it brings about an inference that we do not want to accept; an inference is rejected if it breaks a rule that we do not want to correct. The justification process is a delicate process of doing mutual adjustments between accepted rules and inferences; and in the agreement made, lies the only justification needed for both (Goodman, 1954, p. 64).
Thus, examples and counter-examples are taken seriously in the evaluation of theories. However, it is not enough to show counter-examples to a determined theory when we want to criticize it; one must use them to diagnose the mistakes of the criticized theory and indicate alternatives. This, however, does not go against the fact that the display of counter-examples is an important part of the deeper evaluation of a philosophical theory.
The Flagpole and the Pendulum
We shall begin with the most famous example, already a classic today, of the flagpole shadow (in the literature it has become known simply as Flagpole). Initially proposed by Sylvain Bromberger,7 the example has been repeatedly discussed in the literature on explanation. The problem it presents is really rich source of important insights on the questions that now worry us.
In a first formulation, the example may be described in the following way: suppose a certain flagpole, lit by the sun, which casts its shadow onto the ground. If we take as a law the fact that light travels in a straight line, we can, from the height of the flagpole (h) and from the inclination of the solar rays (q), calculate the length of the shadow (s). This calculation, which may be put in the form of a deduction, can be accepted as an answer to the question "why does such flagpole have a shadow of this height?". We may, also, from the length of the shadow and of the inclination of the solar rays, calculate the height of the flagpole. This calculation, though, does not seem to be an adequate answer to the question "why does such flagpole have a shadow of this height?". Both calculations, however, are adequate to the deductive-nomological model, and can be considered legitimate considerations according to this model (see Salmon et al, 1992 p. 21). This makes us face some problems.
1. Hempel (1965) declares explicitly that explanations may be considered answers to questions such as "why ...?". In the case of the example above, it is difficult to see how to set it in the intended format. The height of the flagpole could answer a question of the kind "Given the length of the shadow (flagpole) and the elevation of the sun, what is the height of the referred flagpole?". At least, we should ask why the formulation is different in this case. We can accept, for the sake of the argument, that the connection between explanations and questions such as "why ...?" has a secondary importance. In this case, we would have a technical conception of the concept of explanation, reducing it to an argument within the deductive-nomological pattern. That is, the ordinary concept of explanation would be replaced by another, more technical one. An explanation would be a kind of calculation in which we can see the relation between events or between its aspects, and that can happen in any direction. One must notice that, in this context, it would be strange to say that we can predict the height of the flagpole due to the lack of clarity in temporal relations. What comes before and what comes after? It is not clear whether we are dealing with a regularity of succession or of coexistence. For Hempel, only regularities of succession can be causal, and a causal explanation is that in which the particular conditions are, temporarily, earlier to the explanandum. The thesis of symmetry between explanation and prediction, discussed previously, would particularly apply to this kind of explanation.
For regularities of coexistence, however, another kind of symmetry becomes evident (we could call it 2nd Thesis of Symmetry): that which allows the interchange between part of the explanans and the explanandum. This interchange may also happen in the causal explanation, although Hempel is ambiguous in this case. For example, we can give a causal explanation of the position of a certain planet from its position at a previous moment (plus the pertinent laws), but we can also calculate the position of the planet at the previous moment from its position at a subsequent moment. In this case, would we have an explanation? Would it be of a non-causal nature? Hempel hesitates. In 1962, he uses the term retrodiction (and not explanation) for the last case we described. He uses the expression deductive-nomological systematization to include prediction, explanation and retrodiction (Hempel, 1962, p. 99). In his most extensive text about explanation, Hempel says:
Any uneasiness in explaining an event with reference to factors that include later occurrences might spring from the idea that explanations of the more familiar sort, such as our earlier examples, seem to exhibit the explanandum event as having been brought about by earlier occurrences; whereas no event can be said to have been brought about by factors some of which were not even realized at the time of its occurrence. Perhaps this idea also seems to cast doubt upon purported explanations by reference to simultaneous circumstances. But, while such considerations may well make our earlier examples of explanation, and all causal explanations, seem more natural or plausible, it is not clear what precise construal could be given to the notion of factors "bringing about" a given event, and what reason there would be for denying the status of explanation to all accounts invoking occurrences that temporally succeed the event to be explained (Hempel, 1965, p. 353-354).
A step further, in his less technical work named Philosophy of Natural Science, he does not simply talk about explanation anymore, but of deductive-nomological explanations to refer to all explanation by subjective subsumption under general laws (Hempel, 1966, p. 70). In the end, we have the strange feeling that everything is reduced to a terminological dispute. There really is a strategic retreat of the author throughout the years. He demands less for his theories, but never says what was wrong with his earlier positions.
What seems to happen here is the following: as the regularities of coexistence have temporal symmetry, Hempel feels more at easy to detach his model from any non-logical objective condition. When we face regularities of succession, Hempel feels that, somehow, time should be taken into account, hence his scruples in naming an explanation a retrodiction. In his works, he nearly always points out the so called causal explanations, though his mature thought is a complete dissolution of the importance of these categories. This may be seen in the previous quote, where he considers the temporal differences of low importance for the explanatory status and, finally, in his attitude by using the technical expression N-D explanation. What seems to be Hempel's final motto is something like it does not matter if we have regularities of succession or of coexistence, an explanation is nothing else than the nomic subsumption of events.8 Perhaps, if he had seen how to capture the causal symmetry without using time, things would have been different.
In fact, it is far from clear why a temporal difference can contribute to the explanatory character. If we had, however, an explanation for causal asymmetry that did not essentially depend on time, we would have the following motto: it does not matter if we have regularities of succession or regularities of coexistence, we can still look for specifically causal explanations in each case. We do not intend our motto to be exact, we have only advanced it in order to highlight the counterpoint to Hempel. First of all, we must remember that we are dealing with explanations of singular events and their aspects, coinciding with the scope of Hempel's theory. Even with this restriction, we do not claim that all explanation of singular facts are causal. Explanations of the whole by its parts (mereological), explanations of identity (that do not involve distinct existences), explanations that suppose the so called determinations of the Cambridge kind9 ("Xanthippe became a widow because Socrates died"), to mention only some of them, all seem to be non-causal explanations (see Kim, 1974). What we want to propose is the following: when we suppose that there is a causal relation involved in a certain context, an explanation within this context must reflect the fundamental characteristics of that relation. In the example of the flagpole, the fundamental dimension neglected by Hempel is directionality (or asymmetry) of causation. In this case, dealt with by Hempel as involving coexistence, we could still indicate a temporal difference in the situation. In connection with this, Salmon, for example, says:
At first glance, we might be inclined to say that this is a case of coexistence: the flagpole and the shadow exist simultaneously. On closer examination, however, we realize that a causal process is involved, and that the light from the sun must either pass or be blocked by the flagpole before it reaches the ground where the shadow is cast (Salmon, 1998, p. 102).
In fact, this interpretation of the example is plausible and Hempel could accept it, as it is made evident in some of his commentaries.10 However, there is still doubt as to whther the causal priority is the temporal priority, and also doubt about the relation of the latter with the explanatory character. In other words, if the difference between the cause and its effect is essentially temporal, what would make the explanation of the effect by the cause different from the explanation of the cause by the effect?
In any case, there are examples in which the temporal difference is not available. The classic case is the one of the relation between the length of the pendulum ( l ) and its period ( T ), in a given gravitational field of acceleration ( g ). Concerning this example, Hempel also considers that it is both possible to explain the period of the pendulum from its length, and the length from the period (Hempel, 1962, p. 94-95). We estimate that this example is greatly comforting to Hempel, since the situation is symmetrical in relation to the only non-logical condition for which he has some respect – time. Thus, he can challenge those who insist on the intuition that only the length of the pendulum explains its period (and not vice-versa), instead of looking for the source of such explanatory asymmetry. He does not seem to consider that the causal priority may not be of a temporal nature and that, therefore, there is the possibility of causation in contexts of coexistence.
This point is also interesting in showing how, from the same example, one can draw opposing conclusions, depending on the initial philosophical commitment. Hempel considers that succession in time is the only thing, besides regularities, that can get into the notion of causation. Thus, the example of the pendulum does not cause problems – we would, simply, be facing a causation case. However, someone who recognizes that there is, in this case, an explanatory asymmetry, may be motivated to search for a non-temporal theory to explain the causal asymmetry and, thus, provide the base for the asymmetry in a certain kind of explanation. An alternative way consists of disconnecting causation and explanation, searching somewhere else for the source of this asymmetry, for example, in pragmatical aspects of new explanations. The examination of this alternative, though, is left for another occasion.
Finally, we would like to examine a deceiving argument that Hempel puts forward to defend his position. Referring to the pendulum case, he says that, if we think normally that an explanation is valid only in one direction, it is because we suppose, wrongly, that we can change the period of the pendulum through the change of its length, but not vice-versa. Against that, he argues that, if the location of the pendulum remains fixed and, therefore, the gravitational acceleration ( g ), we can change the length of the pendulum changing its period. To do so we need only to change the period, modifying first the length of the pendulum and, thus, trivially, changing its length. If g remains constant, any change in l supposes a change in T, and vice-versa (Hempel, 1962, p. 94; and 1965, p. 353-353). This amazing argument, however, is vulnerable if we do not suppose g to be constant. In fact, if g is not constant, a change in T supposes only a change in g or l. We can perfectly suppose that T changed and l remained constant. Hempel could try to restore symmetry, indicating the fact that we can also change l keeping T constant. In this case, we would have to suppose that the variables g and l are correlated so that the variation in one is compensated by a variation in the other. The fact is, however, that we naturally think that the variables l and g are independent, that is, not-correlated (see Hausman, 1998). Thus, the compensation does not happen and Hempel's argument fails. Hempel would need, then, an argument to keep g fixed or for us to suppose that l and g are not independent.11 As far as we know, Hempel's text does not supply such demand. The responsibility for the proof, then, is up to Hempelians.
References
BROMBERGER, S. Why-Questions. In: COLODNY (Ed.). Mind and Cosmos: Essays in Contemporary Science and Philosophy. University of Pittsburgh Press, Pittsburgh, 1966.
GOODMAN, N. [1954]. Fact, Fiction, and Forecast. Cambridge: Harvard University Press, 1983.
HAUSMAN, D. M. Causal Asymmetries. Cambridge: Cambridge University Press, 1998.
HEMPEL, C. G. [1962]. Deductive-Nomological versus Statistical Explanation. In: FETZER (Ed.). The Philosophy of Carl G. Hempel. Oxford: Oxford University Press, 2001.
________. [1966]. Filosofia da Ciência Natural. Rio de Janeiro: Zahar Editores, 1970.
_________. Aspects of Scientific Explanation. In: HEMPEL, C. G. Aspects of Scientific Explanation and the Others Essays in the Philosophy of Science. New York: The Free Press, 1965.
KIM, J. [1974]. Noncausal Connections. In: KIM, J. Supervenience and Mind. Cambridge: Cambridge University Press, 1993.
RUBEN, D. H.. Explaining Explanation. London: Routledge, 1990.
SALMON, W. C. Causality and Explanation. Oxford: Oxford University Press, 1998.
SALMON, W. C. et al. [1992]. Introduction to Philosophy of Science. Indianapolis: Hackett Publishing Company, 1999.
SCRIVEN, M. [1959]. Os truísmos como bases das explicações históricas. In: GARDINER, P. (Ed.). Teorias da História. Lisboa: Fundação Calouste Gulbenkian, 1984.
1 Professor at the Department of Philosophy, Universidade Federal de Ouro Preto. Paper received in May, 2005, and approved in June, 2005. taguiar.bh@terra.com.br
2 In fact, this has full sense only for causal explanations, such as Hempel understands them. In these, the initial conditions or particular circumstances are, temporarily, earlier to the explanandum potential. Even in theses cases, expectability makes full sense only when the derivation that ranges from the initial conditions (and laws) to the potential explanandum occurs before this. In the other cases, expectability, in case the term can be kept, would have to be undestood differently. Perhaps we should talk about expectability as conformity to a calculation. Thus, we would ask "what is the value of x, given the value of y and the relevant laws?", where the realization of x is temporally earlier to the realization of y. We expect the value of the calculation to correspond to what effectively occurred, having in mind that what occurred can be known (for example, through the historical accounts) or not. A concrete example would be the one of an astronomer who calculates the position of a planet in the past through its current position. We can also think of examples in which three inter-related variables have their values realized simultaneously. In this case, we expect the value of any of them, obtained through derivation from the other two to be what happens in reality. Notice that, also in this case, the realization of the values of the variables may be in the present, past or future. Several combinations are possible among the temporal relations of the items that constitute the explanans and the explanadum, and among these and the derivation time.
3 In these cases, Hempel's model is named inductive-statistical model. The inductive-statistical and the deductive-nomological models are generically named lawlike model of cover. In both cases, the explanandum can be rationally expected with certainty or with high probability, and the identification of an explanation with a potential prediction being fundamental.
4 The principle that seems to be working here, and that dates back to Plato, is that the same thing can not explain opposites (see SALMON, 1998, P. 326; RUBEN, 1990, p. 56).
5 Even when he uses the expression measles later symptoms, Hempel does not give the concept of symptom a full causal meaning. He probably uses the term only as a stylistic tool so that he will not repeat the expression measles later manifestations. The distinction between cause and symptom is of great importance in medicine and, in a way, was assimilated by common sense.
6 Considering the possibility of probabilistic predictions, Hempel says: "The basic questions at issue between these different conceptions of probabilistic inference are still the subject of debate and research, and this essay is not the place to attempt a fuller appraisal of the opposing views. The second sub-thesis of the structural identity claim for explanation and prediction will therefore be regarded here as an open question." (Hempel, 1965, p. 376)
7 Originally, the example was proposed in Bromberger (1966), "Why-Questions".
8 We are aware of the difficulties in going from mere regularities to nomic regularities. But this point is not important here, even if we suppose that we have a satisfactory theory of the nomic, the discussed problems remain.
9 This terminology was introduced by Peter Geach in his God and Soul (apud Kim, 1974).
10 "Depending on the context where it is raised, the demand for an explanation might here ask for some kind of causal account of how the flagpole reached this height (...). An account of this kind would be again a special case of causal explanation, invoking among earlier conditions, certain dispositions of the agents involved in the construction of the flagpole" (Hempel, 1962, p. 95).
11 It is clear that we can introduce some mechanism that makes a correlation between l and g, but, in this case, we change the causal structure. The causal structure thus created has new variables and different relations among them.